수치한정발명의 침해판단
- 조회수
- 920
- 작성일
- 2017.01.17
그러나, 현재 우주 탄생 모델의 정설로 인정되고 있는 빅뱅 이론에 의하면, 자연에서 기본이 되는 6가지 상수 가운데 어느 하나만 현재의 값에서 약간 벗어났더라도 우리가 보고 있는 모습의 우주와 생명 자체가 형성되지 않았을 것이라고 한다. 예컨대, 강한 핵력(strong nuclear force)의 크기를 나타내는 ε은 0.007이라는 값을 가지는데, 만일 이 값이 0.006이었다면 우주는 수소로만 가득찬 생명이 없는 무미건조한 공간이 되었을 것이며, 반대로 이 값이 0.008이었다면 수소가 너무 빠르게 핵융합을 일으켜 우주 초기에 모두 소모되어 지금과 같은 별들이 존재할 수 없었을 것이라고 하니, 이는 정량적 특징의 중요성을 새삼 느끼게 하는 흥미로운 사례라 할 것이다.2)
수치한정발명의 문언침해 판단시 고유하게 고려하여야 할 사항으로 수치범위 자체의 해석 또는 특정과 관련된 문제가 있다. 즉, 청구범위에 기재된 수치범위를 고정된 "절대적인" 값으로 볼 것인지, "유효숫자"를 고려한 범위까지 포함하는 것으로 볼 것인지, 아니면 "반올림법"이 적용된 범위까지 포함하는 것으로 볼 것인지 고려할 필요가 있다. 청구청구범위에 측정오차나 유효숫자에 대한 구체적인 정의가 기재되어 있는 경우에는 그에 따를 것이지만, 그렇지 않은 경우에 어떻게 해석하여야 할지의 문제이다. 특히 이는 청구범위의 수치범위와 실시제품의 수치범위가 근접해 있을 때 당사자간에 가장 첨예한 쟁점이 될 소지가 있다. 우리나라에서는 이와 직접적으로 관련된 구체적인 판례나 논의가 발견되지 않으나, 우리나라와 법제와 판례가 상당 부분 공통되는 일본의 경우 특허발명의 '가교제 0.1~1중량%'와 피고 실시제품의 '가교제 1.006중량%' 또는 '가교제 1.013중량%'에 대해 피고 실시제품은 특허발명의 구성의 범위를 초과하는 것이 분명하다고 판단함으로써4) 청구범위에 기재된 수치범위를 "절대적인" 값으로 해석한 사례가 있다.5)
반면, 유럽에서는 Guidelines for Examination G-VI. 8.1 "Error margins in numerical values"에서 수치값의 마지막 자릿수가 정확도를 나타내고, 달리 오차범위가 주어지지 않는다면 최대 오차범위는 마지막 자릿수에 "반올림법"을 적용하여 결정하여야 한다고 한다. 또한 최근 영국의 항소법원 판결(Smith & Nephew v Convatec Technologies Inc. [2015] EWCA Civ 607)에서는, "청구범위에서 1%~15%의 수치범위는 반올림법을 적용할 때 그 하한치 1%가 0.5% 이상의 수치를 포함하는 것으로 해석되고, 따라서 0.77%를 사용하는 피고회사의 공정은 특허권을 침해하는 것이다."라고 판단했다.6) [1심 법원에서는 유효숫자법을 적용하여, 유효숫자가 1개인 하한치 1%는 0.95 이상 1.5 미만%를, 유효숫자가 2개인 상한치 15%는 14.5 이상 15.5 미만%를 의미하므로, 침해가 아니라고 판단한 바 있다].
수치범위의 해석과 관련된 또하나의 이슈는 수치범위에 기재된 "약"(about)의 문제이다. 우리나라는 청구항에 "약"이 기재된 경우, 수치범위를 불명료하게 한다는 거절이유가 거의 예외 없이 통지되고 이 경우 "약"을 삭제하는 것이 통상의 실무이지만 일부 출원의 경우에는 "약"이 기재된 채로 그대로 등록되는 사례도 있고, 구미의 경우에는 청구항에 "약"이 기재된 사례를 더욱 빈번히 발견할 수 있다. "약"의 해석도 청구범위의 해석의 기본 원칙에 입각하여 이루어져야 할 것이고, 따라서 명세서에 "약"의 정의가 있다면 그 정의에 따라 수치범위를 더 특정할 수 있다. 만일 명세서에 그러한 정의가 마련되어 있지 않다면 통상의 기술자의 인식에 따라야 할 것이다.
우리나라에서는 "부직포 두께에 있어서 이 사건 특허발명은 ‘약 0.8~1.5㎜ 정도’인데 ㈎호 발명은 0.1~0.79㎜로서 미세한 차이가 있으나 이는 부직포의 제조과정에서 나타날 수 있는 오차 범위 내에 해당하며"라고 한 판례가 있으나(대법원 2003. 12. 12. 선고 2002후2181 판결), "약"의 해석이 크게 쟁점이 되거나 보다 구체적으로 다루어진 판례는 발견되지 않는다. 미국에서는 『"약"이라는 단어는 청구범위에서 통일된 의미를 가지지 아니하고, 그 의미는 특정 사안의 기술적인 사실관계에 따라 달라질 것이다. "약"이라는 단어의 사용으로 인하여 그 한정된 파라미터로 수치범위를 엄격하게 제한하는 것을 방지한다.』라는 것이 CAFC에서 발전된 접근법이고[Pall Corp. v. Micron Separations, Inc., 66 F.3d 1211, 1217 (Fed. Cir. 1995) 및 MPEP 2111], "약"은 과학에서 통용되는 "반올림법"이 적용되는 범위를 의미하는 것으로 통상 해석할 수 있다고 한다.7)


IV. 결론 및 실무에 있어서의 시사점
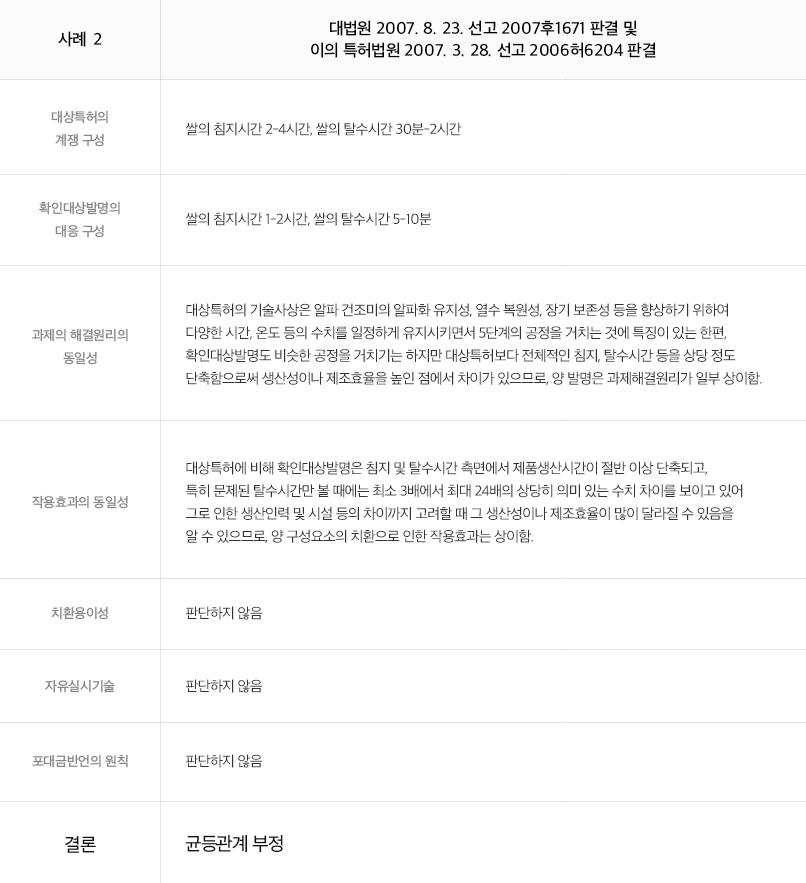
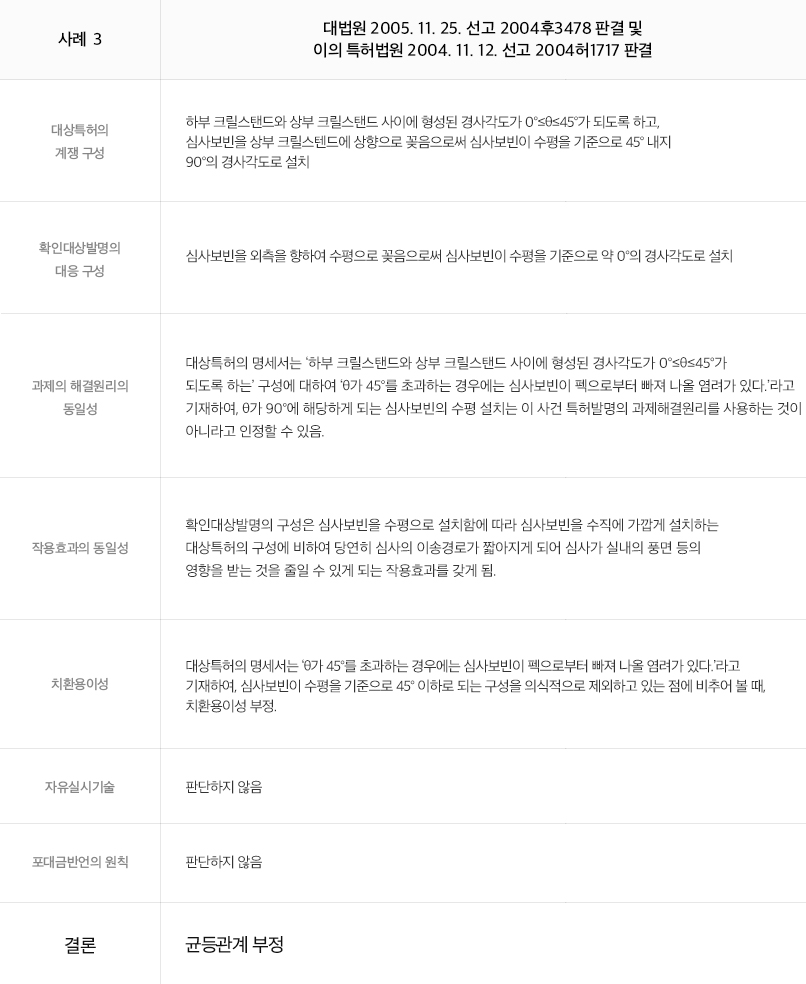
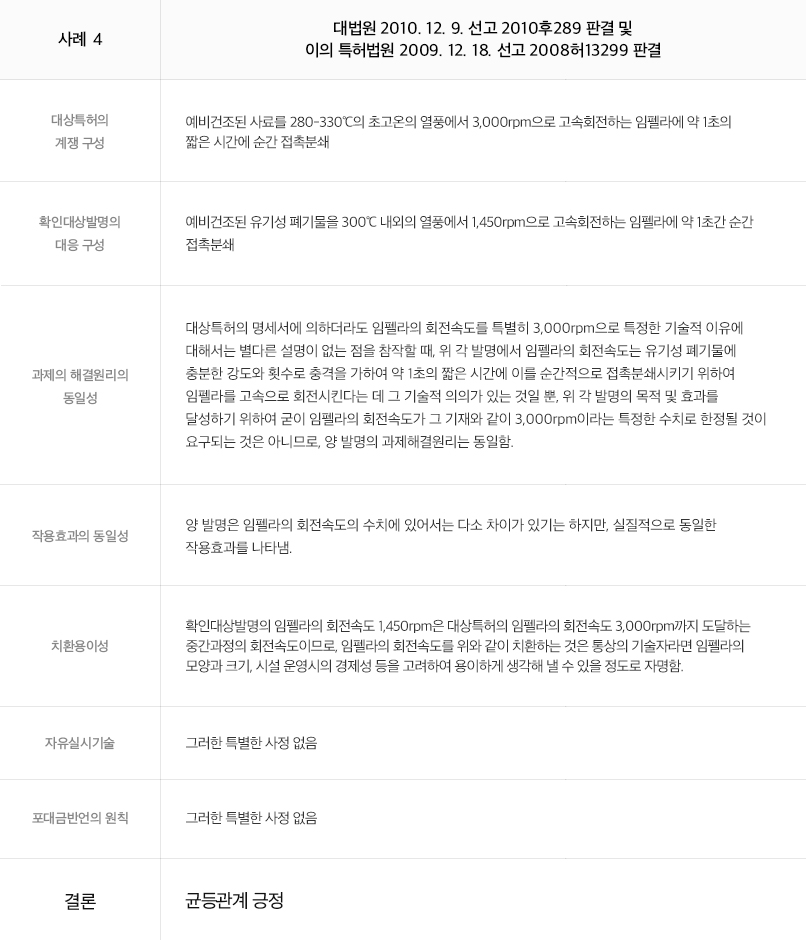
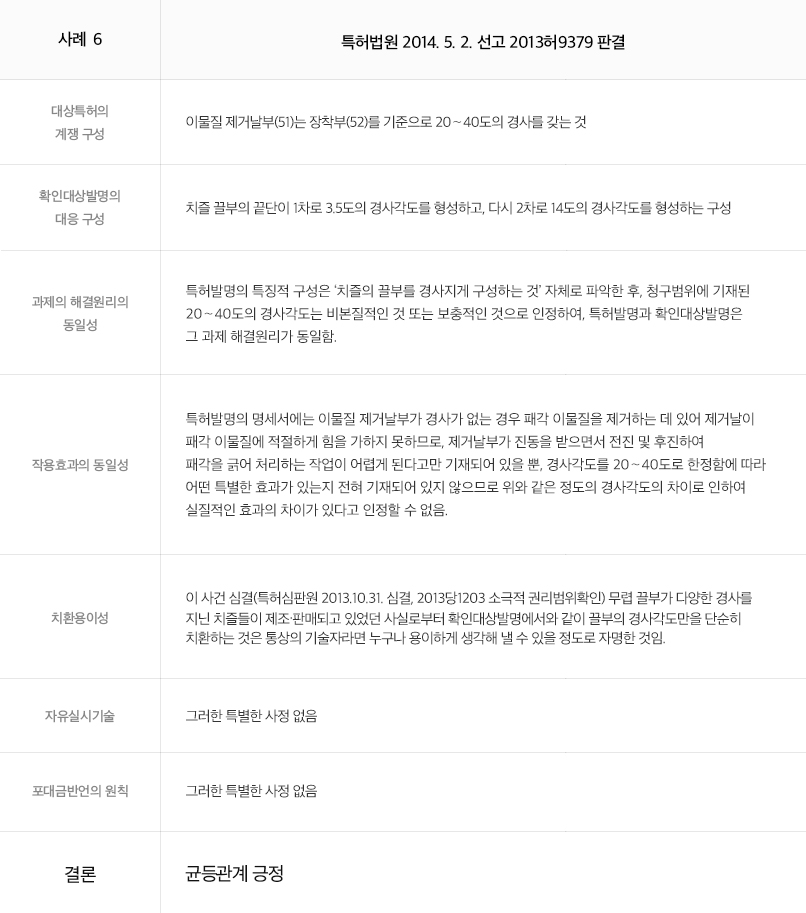
출원인 및 대리인의 입장에서, 수치한정발명의 경우 필수적으로 수치한정의 기술적 의의를 출원 당시의 명세서에 분명히 기재하고, 그 효과(이질적 효과 또는 동질이지만 현저한 효과(임계적 의의))를 입증할 수 있는 실험 자료도 최대한 출원 당시의 명세서에 실시예 및 비교예로 포함될 수 있도록 하거나, 적어도 심사관의 거절이유에 대응하여 제출할 수 있도록 준비해 둘 필요가 있다는 점을 먼저 명심하여야 할 것이다. 또한, 수치한정발명은 그 속성상 문언침해 여부의 판단은 용이한 한편, 청구된 수치범위 내외의 기술적 특징 및 효과의 차이점이 강조된다는 점에서 다른 발명들에 비해 균등론이 적용될 여지는 그만큼 적을 수밖에 없다고 생각된다. 따라서 등록 후 수치한정발명의 권리행사 가능성을 제고하기 위해서는 출원 당시의 명세서에 수치한정의 기술적 의의를 보다 풍부하게, 그러나 어떤 원리에 반드시 구속받지는 않게 기재하여 발명의 확장 가능성을 열어 두는 것이 균등론에서 "과제해결원리의 동일성"을 강조하는 판례의 입장을 고려할 때 실무상 중요하다고 생각된다.
V. 참고문헌
Big Bang: The Origin of the Universe", Simon Singh
수치한정발명과 균등론", 양인수, 지식재산연구 제11권 제4호(2016. 12)
1) 그러나 그는 불과 10여년만에 다름아닌 자신의 발견에 근간하여 아인슈타인의 상대성이론이 제창되고, 기존의 물리학 체계와 통념으로는 전혀 설명될 수 없는 양자역학이 출현하는 등, 19세기 말에 완성된 고전물리학의 근본을 송두리째 뒤흔드는 현대물리학이 태동하는 20세기 초의 격변의 시대를 현장에서 직접 목도해야만 했다.
2)"Just Six Numbers: The Deep Forces that Shape the Universe", Martin Rees
3) 신규성에 관한 것으로서, 대법원 2013. 5. 24. 선고 2011후2015 판결; 진보성에 관한 것으로서 대법원 2010. 8. 19. 선고 2008후4998 판결.
4) 東京地裁 平成17年5月30日, 平成15年(ワ)第25968号. 균등침해 여부와 관련하여서도, 발명의 설명의 기재 및 출원경과를 참작하여 볼 때, '가교제를 0.1~1중량%로 함유하는 구성'은 본질적인 부분에 해당하는 것이기 때문에, 피고 실시제품은 특허발명의 구성과 균등한 것으로도 볼 수 없다고 판시하였다.
5) 발명은 자연법칙을 이용한 기술적 사상(idea)의 창작이라는 점에서, 그러한 기술적 사상을 글로써 표현하여 나타낸 청구범위에 수치범위가 기재되어 있다면, 그 수치범위는 발명자가 의도한 이상적인(ideal) 추상적 범위로서, 즉 일응 "절대적인" 것으로 해석하여야 하고, 그 수치범위 밖의 범위는 균등론 적용 여부의 판단 영역에 속하는 것으로 보는 사고방식이 우리나라 법제상으로도 타당하다는 것이 사견이다.
6) 그러나, 이 사례에서는 청구항에 기재된 하한치인 1%의 절반에 불과한 0.5%까지 청구범위에 속하는 것으로 해석하였다는 점에서, 반올림법을 만고불변의 법칙이라고 선뜻 받아들이기도 어려운 면이 존재한다.
7) "Patent Claim Construction", Robert C. Kahrl, pp. 4-195
8) 대법원 2014. 7. 24. 선고 2012후1132 판결
 법무법인 다래
법무법인 다래